Zmiana wartości pieniądza w czasie jest naturalnym procesem nie tylko dla osób zawodowo zajmujących się finansami. Wpływ czasu na wartość lokowanych zasobów pieniężnych, jak również na wartość zadłużenia, to jeden z ważniejszych czynników, które decydują o opłacalności decyzji podejmowanych przez przedsiębiorstwa, ale także przez osoby fizyczne. Zmiana wartości pieniądza w czasie jest zjawiskiem powszechnym i wiąże się m.in. z kosztem kapitału, a więc stopą zwrotu oczekiwaną przez dawcę tego kapitału. Pominięcie zjawiska zmian wartości pieniądza w czasie przy podejmowaniu wszelkich decyzji związanych z lokowaniem lub pożyczaniem kapitału gotówkowego może doprowadzić do negatywnych konsekwencji w zakresie efektywności. W niniejszym artykule zaprezentowane zostały podstawowe funkcje finansowe wykorzystywane w arkuszach kalkulacyjnych, służące określaniu zmian wartości pieniądza w czasie.

Wartość przyszła (FV)
Wartość przyszła (ang. FV, Future value) to wartość inwestowanych przepływów pieniężnych po określonej stopie oprocentowania na określony czas na końcu tego okresu. Z punktu widzenia inwestora (kapitałodawcy) wartość pieniądza w czasie powinna wzrastać, żeby zrekompensować czas oraz ryzyko związane z udostępnieniem kapitału, zatem przyszła wartość powinna być z reguły wyższa od sumy gotówki wpłacanej przez inwestora lub też otrzymywanej przez pożyczkobiorcę.
Chcąc wyznaczyć wartość przyszłą w arkuszu kalkulacyjnym, należy wykorzystać formułę FV: FV (stopa;liczba_okresów;rata;[wb];[typ]).
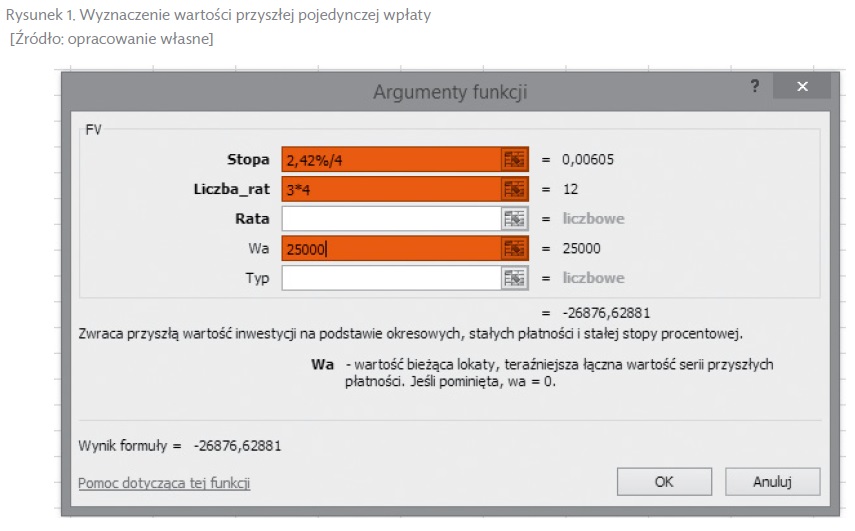
Załóżmy, że planujemy założyć lokatę, której oprocentowanie wynosi 2,42% w skali roku. Planowana wartość inwestycji to 25 000 PLN. Całość wkładu ma zostać wpłacona jednorazowo na 3 lata. Bank nalicza odsetki co kwartał. Wyznaczenie przyszłej wartości przy powyższych założeniach z zastosowaniem formuły FV przedstawia rysunek 1.
Żeby wyznaczyć przyszłą wartość pojedynczej płatności, należy postępować zgodnie z dalszymi wskazówkami:
- W polu „Stopa” należy podać oprocentowanie dla podokresu kapitalizacji (ponieważ w podanym przykładzie zastosowanie ma kapitalizacja miesięczna, należy podać stopę zwrotu dla jednego kwartału, która w analizowanym przypadku wynosi 2,42%/4).
- W polu „Liczba_rat” należy wpisać liczbę podokresów, na które decydujemy się dokonać wpłaty. Okresy te powinny korespondować z wartością podaną w polu „Stopa”, zatem jeśli stopa dotyczy kwartału, a lokata zakładana jest na trzy lata, w polu tym należy podać liczbę kwartałów w tym okresie.
- Ostatnim zakresem wymagającym wypełnienia jest „Wp”, gdzie należy podać wartość, którą planujemy wpłacić na lokatę (w prezentowanym przykładzie jest to wartość 25 ٠٠٠ PLN).
Otrzymana wartość 26 876,63 PLN to kwota, którą inwestor otrzyma po upływie trzech lat na opisanych powyżej warunkach.
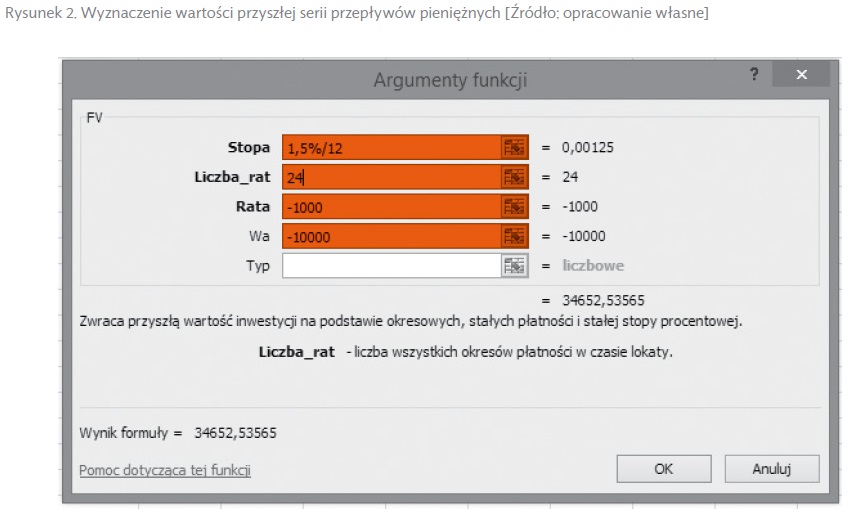
Formuła FV umożliwia także wyznaczenie wartości przyszłej serii przepływów pieniężnych. Przyjmijmy sytuację, w której posiadamy 10 000 PLN na lokacie oprocentowanej 1,5% w skali roku. Dodatkowo planujemy dokonywać na koniec każdego miesiąca wpłaty w wysokości 1000 PLN w ciągu 2 lat. Zakładając miesięczną kapitalizację odsetek, możemy wykorzystać w opisywanym przykładzie formułę FV w celu oszacowania wartości środków pieniężnych na lokacie po dwóch latach. Sposób zastosowania formuły przedstawia rysunek 2.

Pozostałe 65% artykułu dostępne jest dla zalogowanych użytkowników serwisu.
Jeśli posiadasz aktywną prenumeratę przejdź do LOGOWANIA. Jeśli nie jesteś jeszcze naszym Czytelnikiem wybierz najkorzystniejszy WARIANT PRENUMERATY.
Zaloguj Zamów prenumeratę Kup dostęp do artykułuMożesz zobaczyć ten artykuł, jak i wiele innych w naszym portalu Controlling 24. Wystarczy, że klikniesz tutaj.